Generalized assignment problem
In applied mathematics, the maximum generalized assignment problem is a problem in combinatorial optimization. This problem is a generalization of the assignment problem in which both tasks and agents have a size. Moreover, the size of each task might vary from one agent to the other.
This problem in its most general form is as follows:
There are a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost and profit that may vary depending on the agent-task assignment. Moreover, each agent has a budget and the sum of the costs of tasks assigned to it cannot exceed this budget. It is required to find an assignment in which all agents do not exceed their budget and total profit of the assignment is maximized.
Contents |
Special cases
In the special case in which all the agents' budgets and all tasks' costs are equal to 1, this problem reduces to the maximum assignment problem. When the costs and profits of all agents-task assignment are equal, this problem reduces to the multiple knapsack problem. If there is a single agent, then, this problem reduces to the Knapsack problem.
Definition
In the following, we have n kinds of items, 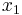 through
through 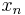 and m kinds of bins
and m kinds of bins 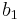 through
through 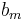 . Each bin
. Each bin 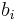 is associated with a budget
is associated with a budget 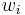 . For a bin
. For a bin 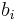 , each item
, each item 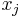 has a profit
has a profit 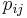 and a weight
and a weight 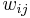 . A solution is subset of items U and an assignment from U to the bins. A feasible solution is a solution in which for each bin
. A solution is subset of items U and an assignment from U to the bins. A feasible solution is a solution in which for each bin 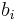 the weights sum of assigned items is at most
the weights sum of assigned items is at most 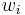 . The solution's profit is the sum of profits for each item-bin assignment. The goal is to find a maximum profit feasible solution.
. The solution's profit is the sum of profits for each item-bin assignment. The goal is to find a maximum profit feasible solution.
Mathematically the generalized assignment problem can be formulated as:
- maximize
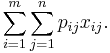
- subject to
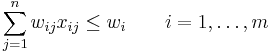 ;
;
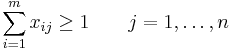 ;
;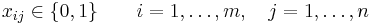 ;
;
The generalized assignment problem is NP-hard, and it is even APX-hard to approximate it. Recently it was shown that an extension of it is (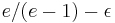 ) hard to approximate for every
) hard to approximate for every  .
.
Greedy approximation algorithm
Using any algorithm ALG  -approximation algorithm for the knapsack problem, it is possible to construct a (
-approximation algorithm for the knapsack problem, it is possible to construct a (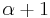 )-approximation for the generalized assignment problem in a greedy manner using a residual profit concept. The algorithm constructs a schedule in iterations, where during iteration
)-approximation for the generalized assignment problem in a greedy manner using a residual profit concept. The algorithm constructs a schedule in iterations, where during iteration  a tentative selection of items to bin
a tentative selection of items to bin 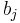 is selected. The selection for bin
is selected. The selection for bin 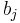 might change as items might be reselected in a later iteration for other bins. The residual profit of an item
might change as items might be reselected in a later iteration for other bins. The residual profit of an item  for bin
for bin 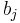 is
is 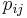 if
if  is not selected for any other bin or
is not selected for any other bin or 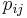 –
– 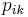 if
if  is selected for bin
is selected for bin 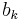 .
.
Formally: We use a vector  to indicate the tentative schedule during the algorithm. Specifically,
to indicate the tentative schedule during the algorithm. Specifically, ![T[i]=j](/2012-wikipedia_en_all_nopic_01_2012/I/2e5860742f2e1f1594a4e13d393d321f.png) means the item
means the item  is scheduled on bin
is scheduled on bin 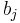 and
and ![T[i]=-1](/2012-wikipedia_en_all_nopic_01_2012/I/1b0333e98862ae2000bb04c4cfcbac58.png) means that item
means that item  is not scheduled. The residual profit in iteration
is not scheduled. The residual profit in iteration  is denoted by
is denoted by 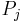 , where
, where ![P_j[i]=p_{ij}](/2012-wikipedia_en_all_nopic_01_2012/I/e6be29ba694a7b42da3a5ea507d7fe9e.png) if item
if item  is not scheduled (i.e.
is not scheduled (i.e. ![T[i]=-1](/2012-wikipedia_en_all_nopic_01_2012/I/1b0333e98862ae2000bb04c4cfcbac58.png) ) and
) and ![P_j[i]=p_{ij}-p_{ik}](/2012-wikipedia_en_all_nopic_01_2012/I/3cb86b13327614f1af1f4874b722098b.png) if item
if item  is scheduled on bin
is scheduled on bin 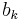 (i.e.
(i.e. ![T[i]=k](/2012-wikipedia_en_all_nopic_01_2012/I/573b2ee121dba2a7c4672f922e2d7f1e.png) ).
).
Formally:
- Set
![T[i]=-1](/2012-wikipedia_en_all_nopic_01_2012/I/1b0333e98862ae2000bb04c4cfcbac58.png) for all
for all 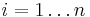
- For
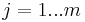 do:
do:
- Call ALG to find a solution to bin
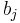 using the residual profit function
using the residual profit function 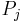 . Denote the selected items by
. Denote the selected items by 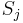 .
. - Update
 using
using 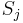 , i.e.,
, i.e., ![T[i]=j](/2012-wikipedia_en_all_nopic_01_2012/I/2e5860742f2e1f1594a4e13d393d321f.png) for all
for all 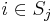 .
.
- Call ALG to find a solution to bin
See also
References
- Reuven Cohen, Liran Katzir, and Danny Raz, "An Efficient Approximation for the Generalized Assignment Problem", Information Processing Letters, Vol. 100, Issue 4, pp. 162-166, November 2006.
- Lisa Fleischer, Michel X. Goemans, Vahab S. Mirrokni, and Maxim Sviridenko, "Tight Approximation Algorithms for Maximum General Assignment Problems", SODA 2006, pp. 611-620.
- Hans Kellerer, Ulrich Pferschy, David Pisinger, Knapsack Problems , 2005. Springer Verlag ISBN 3-540-40286-1